Thurston norm: Part I

February 28, 2024

Let $(M, \partial M)$ be a compact, oriented $3$-manifold. We shall say a compact surface $(S, \partial S) \subset M$ is properly embedded if $S \subset M$ is an embedded surface and $\partial S \subset \partial M$ is a collection of embedded curves. A properly embedded oriented surface may be triangulated to obtain a singular $2$-cycle relative to $\partial M$, which represents its fundamental class $[(S, \partial S)] \in H_2(M, \partial M; \Bbb Z)$. Conversely, suppose we have a class $\alpha \in H_2(M, \partial M; \Bbb Z)$. Then its Poincare dual $\mathrm{PD}(\alpha)$ gives rise to a map $\phi : M \to S^1$ by chasing the sequence isomorphisms:

\[\displaystyle H_2(M, \partial M; \Bbb Z) \cong H^1(M, \Bbb Z) \cong \mathrm{Hom}(\pi_1(M), \Bbb Z) \cong [M, S^1]\]

Let $p \in S^1$ be a regular value of $\phi$. Then $S = \phi^{-1}(p)$ satisfies $[(S, \partial S)] = \alpha$. One might then ask what is the minimum possible complexity of a surface representing a given relative second homology class. One measure of such a complexity is genus, but since our surfaces have boundary, we would like to consider the negative part of the Euler characteristic instead.

Definition. For $\alpha \in H_2(M, \partial M; \Bbb Z)$, the Thurston norm of $\alpha$ is defined as

\[\displaystyle \|\alpha\| = \mathrm{inf}_S \sum_{S_i \subset S} \max\{0, -\chi(S_i)\},\]

where $S$ varies over all surfaces such that $\alpha = [(S, \partial S)]$ and $S_i$ are connected components of $S$.

Notice that sphere, disk, annulus and torus components of a surface contribute nothing to the norm. In some sense, this is intentional: one is searching for surfaces of minimal complexity to cut $M$ along after it has already been cut along all the two-sided incompressible spheres (i.e., prime decomposition) and a minimal collection of two-sided incompressible tori (i.e., JSJ decomposition). Nevertheless, formally ignoring these cases by not assigning them any importance in the norm allows one to define it in full generality.

Observation. Let $M$ be irreducible (i.e., all embedded spheres either bound a ball or are boundary-parallel). If $(S, \partial S) \subset M$ realizes Thurston norm in its homology class (we shall say: $(S, \partial S)$ minimizes the norm), then $S$ is incompressible.

Proof. Suppose not. Irreducibility guarantees we can assume there are no spherical components. Then there must be a closed curve $\gamma \subset S$ which is not nullhomotopic in $S$, but is nullhomotopic in $M$. Then the loop theorem implies $\gamma$ must also bound a disk $D$ (called a “compressing disk”) in $M$. Consider a thickening of $S \cup D \subset M$ and take one of the boundary components to obtain a “compression” of $S$ along $D$, which we shall call $S'$. Note $\chi(S') = \chi(S) + 2$. If $\gamma$ is non-separating, we observe that $S'$ cannot be a sphere by irreducibility of $M$. If $\gamma$ is separating, say $S' = S_1' \cup S_2'$, then $S_1', S_2'$ cannot be spheres as $\gamma \subset S$ is essential. Therefore, $(S', \partial S')$ has total negative Euler characteristic strictly less than that of $(S, \partial S)$, contradicting the hypothesis that $(S, \partial S)$ is a norm-minimizer.

Remark. A surface $(S, \partial S) \subset M$ is said to be boundary-compressible if there is an embedded disk $D \subset M$ (called a “boundary-compressing disk”) such that $\partial D = \alpha \cup \beta$ is a union of a pair of arcs sharing endpoints such that $D \cap S = \alpha$ is an essential arc in $S$ and $D \cap \partial M = \beta$. Since compressing along a boundary compressing disk is tantamount to cutting $S$ along $\alpha$, the result is a surface $S’$ such that $\chi(S’) = \chi(S) + 1$. If $M$ is boundary-irreducible (i.e., $\partial M$ has no spherical components and is $\pi_1$-injective in $M$), we can rule out disk components in $S’$ by an analogous argument as above. Therefore, in this case the norm-minimizing surfaces must also be boundary-incompressible.

Why stop here? We may define for any rational class $\alpha \in H_2(M, \partial M; \Bbb Q)$, $|\alpha| = |k \alpha|/k$ where $k$ is an integer so that $k\alpha$ is integral. We may even extend $|\cdot|$ to all of $H_2(M, \partial M; \Bbb R)$: simply write a real class as a real linear combination of an integral basis of $H_2(M, \partial M; \Bbb Z)$, and approximate the coefficients by rationals. There are two things to be checked in order to ensure this is well-defined:

Is it true that $|k[S]|=k|[S]|$ for integer $k$?
Is it true that $|[S] + [S’]| \leq |[S]| + |[S’]|$?

Check 1. Suppose $S’ = \phi^{-1}(p)$ is a surface that represents $k[S]$, where $\phi :M \to S^1$ corresponds to the class $k \mathrm{PD}[S] \in H^1(M; \Bbb Z)$. This map lifts along the $k$-fold covering map $S^1 \to S^1$. Let us denote the lift as $\tilde{\phi} : M \to S^1$. Then $S$ is disjoint union of the surfaces $S_i = \tilde{\phi}^{-1}(p_i)$, $1 \leq i \leq k$, each in the homology class of $[S]$. Moreover, if we choose $S’$ to be a norm-minimizer, each connected component $S_i$ has to be a norm-minimizer as well. Thus, $|k[S]| = k |[S]|$.

Check 2. Suppose $M$ is irreducible and $\partial M = \emptyset$. We choose $S, S’$ to be norm-minimizers, which implies they are incompressible by an earlier observation. We put the surfaces in general position. Note that $S \cap S’$ consists of disjoint simple closed curves as $S, S’ \subset M$ are embedded. Suppose $\gamma$ is a closed curve in the intersection which is nullhomotopic in $M$, then by incompressibility it is nullhomotopic in both $S, S’$. Without loss of generality, say $\gamma$ is innermost in $S$, i.e., there’s no other loop in the Jordan disk bounded by $\gamma$ in $S$ that is in the intersection locus $S \cap S’$. The sphere co-bounded by the disk bounding $\gamma$ in $S, S’$ respectively bounds a ball by irreducibility of $M$, and we may push $S$ to the boundary of the ball to reduce the cardinality of the intersection locus. After doing this finitely many times, we are left with an intersection locus consisting only of disjoint simply closed curves which are essential in both $S$ and $S’$. The local picture near the intersection is the same as $\mathbf{X} \times S^1$ where $\mathbf{X}$ is the letter X. We replace this by $\pmb{)(} \times S^1$ in a way that the resulting surface is oriented. The resulting surface $S’’$ is obtained by cutting $S, S’$ along certain disjoint essential simple closed curves and gluing along the seams. Therefore, $\chi(S’’) = \chi(S) +\chi(S’)$. Moreover, no component of $S’’$ can be a sphere, as that would imply one of the seams in $S$ or $S’$ is non-essential. Observe $S’’$ represents the homology class $[S] + [S’]$. Therefore, $|[S] +[S’]| \leq |[S]| + |[S’]|$, as desired. If $\partial M \neq \emptyset$, and $M$ is irreducible and boundary-irreducible, then from the remark below the observation above, we may likewise conclude the same inequality.

The verifications above implies $| \cdot |$ is a well-defined semi-norm on $H_2(M, \partial M; \Bbb Q)$ and as such can be continuously extended to a semi-norm on $H_2(M, \partial M; \Bbb R)$. Note that if $(M, \partial M)$ is a hyperbolic $3$-manifold with cuspidal boundary, this is in fact a norm, as there cannot be any essential spheres, tori, disks or annuli inside the manifold, which are precisely the surfaces on which the Thurston norm vanishes.

Definition. The Thurston norm-ball of $(M, \partial M)$ is defined to be the unit ball in $H^2(M, \partial M; \Bbb R)$ under the Thurston norm.

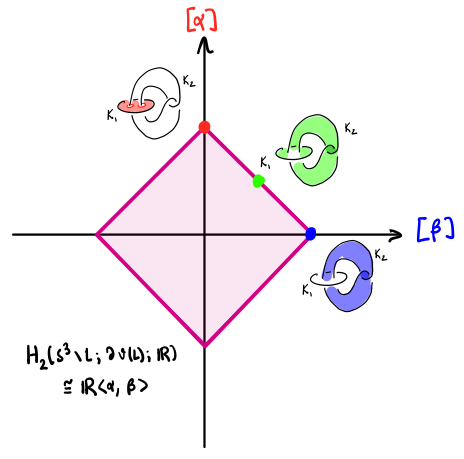
Figure: Thurston norm-ball for the Whitehead link.

As an example, we try to compute the Thurston norm for the complement $S^3 \setminus \nu(L)$ of the Whitehead link $L \subset S^3$. The real homology of the complement is a real vector space of rank $2$, generated by Poincare dual to the meridians of each of the components $K_1, K_2$ indicated in the picture. These are given by the thrice-punctured sphere $\alpha$ bounded by $K_1$, and the punctured torus $\beta$ bounded by $K_2$, respectively, indicated by the red and blue surfaces in the picture. Each of these have Euler characteristic $-1$ and are norm-minimizing, so they are in the unit sphere for the Thurston norm. Symmetrically, $-\alpha, -\beta$ are also elements in the unit sphere. In the picture we also have a green dot which corresponds to the class of $(\alpha + \beta)/2$. Note that $\alpha + \beta$ is represented by the surface drawn in green, given by an oriented sum of the surfaces $\alpha$ and $\beta$. This is a “Seifert surface” for the Whitehead link, and its Euler characteristic is $-2$ (sum of the ones for $\alpha, \beta$). In fact, we shall show next time that the entire line segment connecting $(1, 0)$ and $(0, 1)$ is contained in the unit sphere. Therefore, the unit norm-ball is the magenta diamond above.

Exercise. Can you imagine a norm-minimizing representative of $2 \alpha + \beta$? How about $5 \alpha + 3 \beta$?